The following page is the summary of the entire first scientific checkpoint project, the topic of which is "Time evolution in Quantum Mechanics"
Over the course of the following weeks, it will be slowly expanded with additions of new explanations, videos, papers and/or paper contents, interactive quizzes and more educational materials.
Before we begin with our advanced Quantum Mechanical journey, we first need to start with the basics.
To make sure we've all gotten a good foundation for what we're about to do, we need to start with something simple. The mathematics we'll use in order to develop our physical theories, and there are a couple of tools we need to add to our belt in order to formulate the aformentioned theories properly, so
Physics is all about predicting the evolution of systems or put another way, the change in certain quantities; enter the derivative. Although a topic widely known, one can't have too many refreshers and for that we have just the perfect video going over the geometric intuition behind derivatives and the rules associated to them in a visually appealing way.
But ordinary derivatives on their own aren't enough, in physics we mostly deal with a tad more specific kind of derivative and that is, the partial derivative.
Partial derivatives are characterised by operating in a narrower way in comparison to their ordinary counterparts, a point illustrated in the following video
This concludes our introduction to derivatives, for a deeper understanding there exists a

One last thing to help us on our journey would be to develop an intuition for what those derivatives would mean, it will be particularly useful in the future with more complicated formalisms, but it won't hurt to introduce now.
Having covered derivatives puts us in the prime position to start discussing every physicists beloved tool, The Taylor Series
Briefly illustrated in the following video
I think the utility of The Taylor Series can be easily seen.
Linear Algebra will be the most crucial mathematical concept of the quantum formalism, so understanding it will be of utmost importance, which is why it is encouraged for the reader to pay careful attention to the sources provided.
First source will once again, be a video, which should hopefully provide a decent enough intuition behind the notation of bra's and ket's
The video, light as it may be, will not be nearly sufficient to cover the background required in order for us to get a firm grip on Quantum Mechanics, a deeper understanding of linear algebra is crucial, which is why the

We're going to start as simple as we can, with the simplest physical system, that is, the harmonic oscilaltor.
This Harmonic Oscillator will form a backbone of this checkpoint, serving as an example of every formalism we'll go over to solidify our understanding of how they function, and so as such, to first familiarise ourselves with this system, let's start with a Newtonian formalism.
In this scenario we define our Oscillator as follows,
This definition ensures that as our Oscillator moves away from the origin, it experiences a force pushing it back.
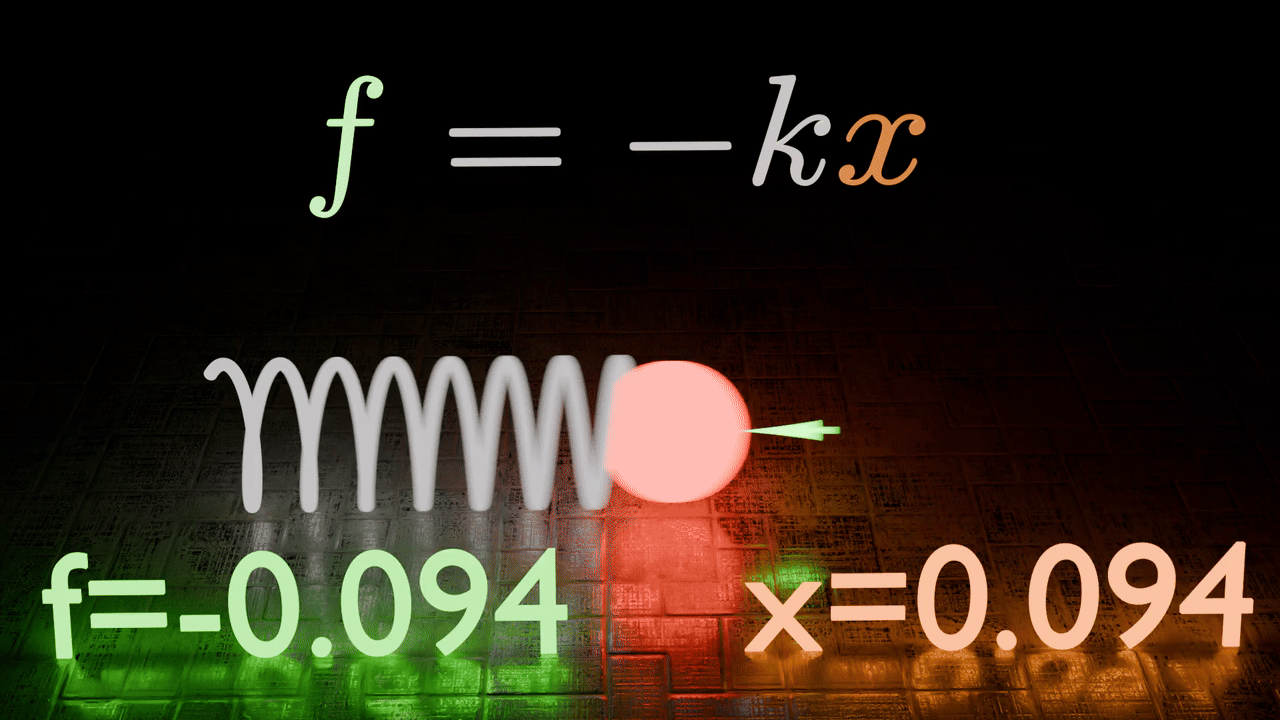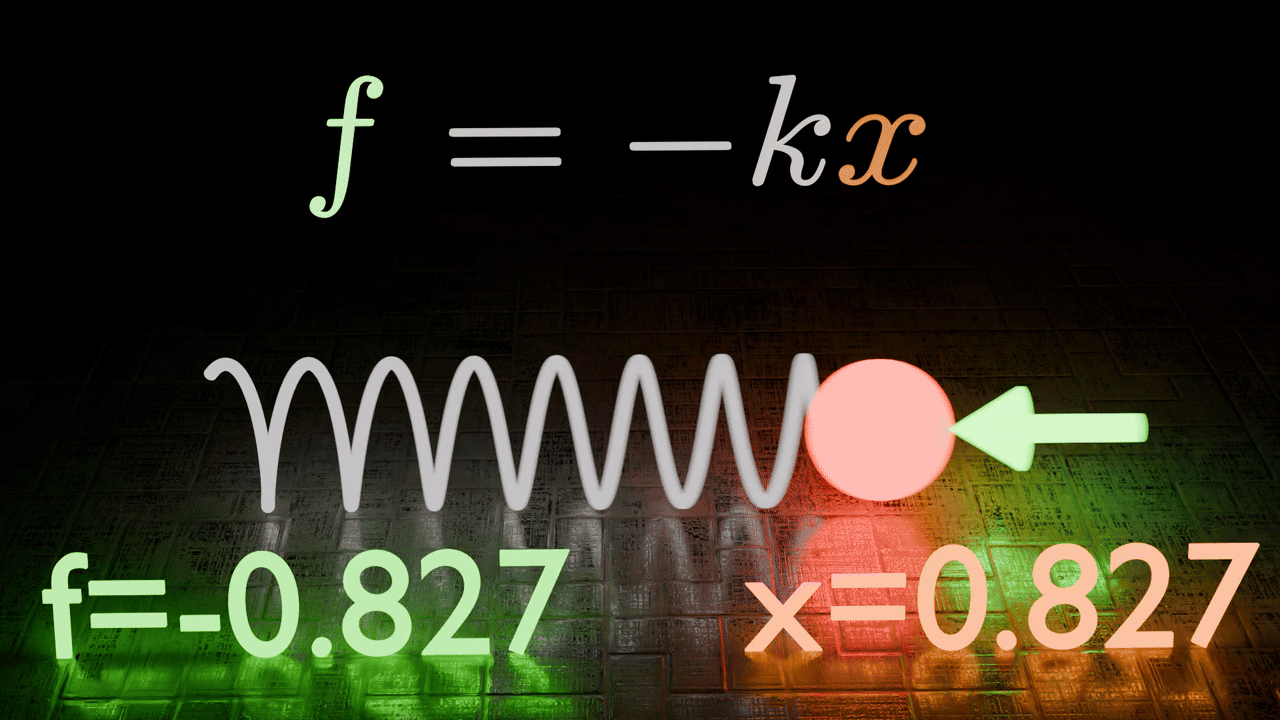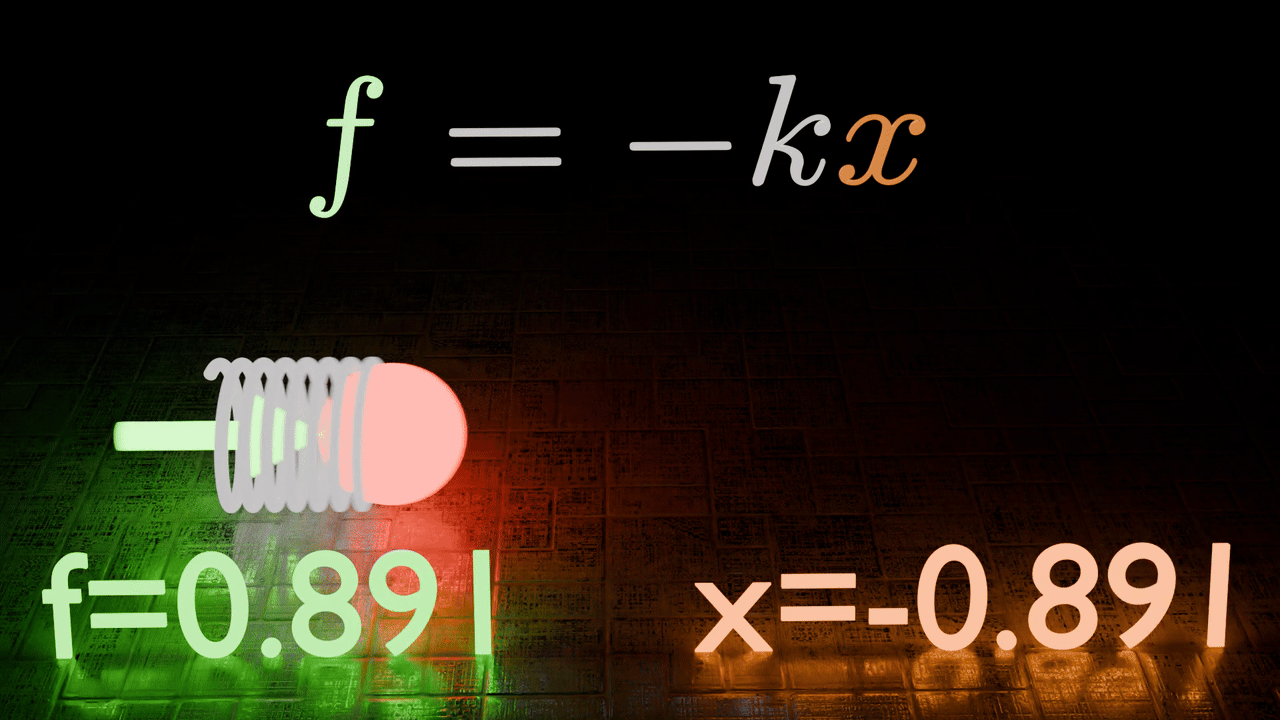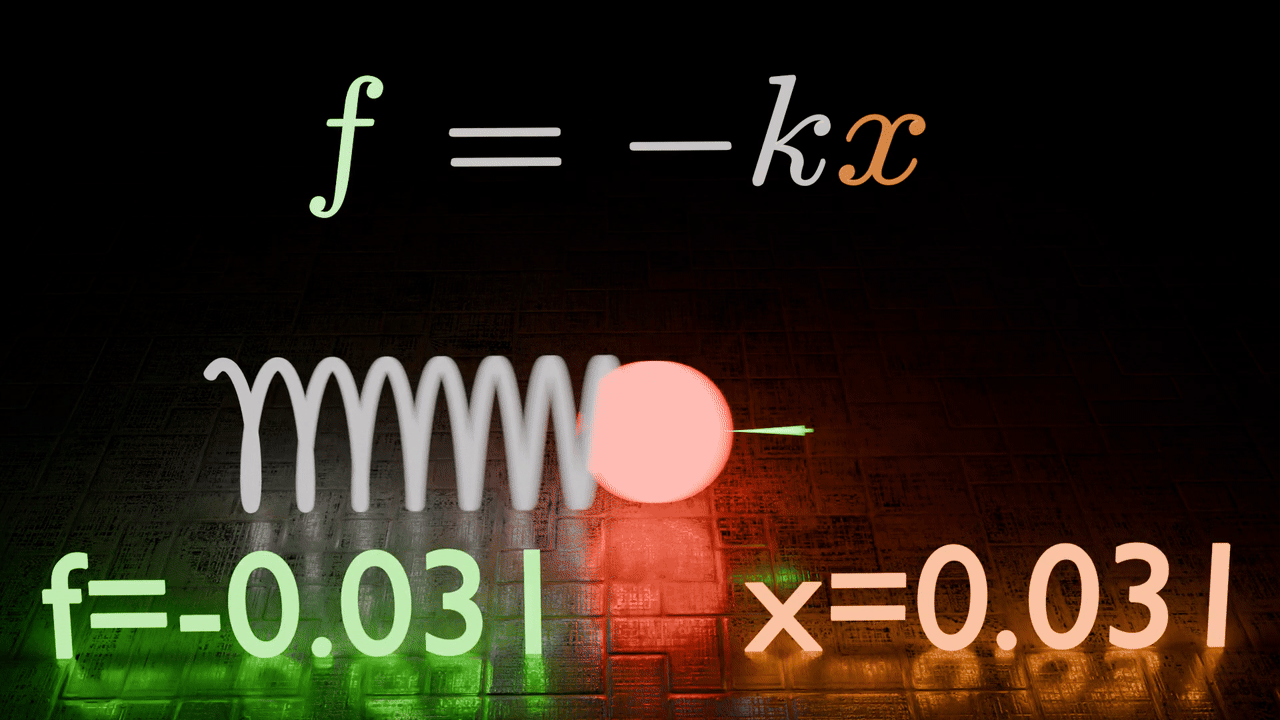
Using our Newtonian formalism we can describe it in the following equation.
which when followed to it's logical conclusion gives us
The solved system.
As we have seen so far, states play an important role in quantum mechanics. We have used them in combination with the hamiltonian, position and momentum operators to obtain the relevant eigenvalues, plainly speaking, they are the operatee's which give us the actual scalar values we use in order to interpret the results of our physical experiments.
It's easy to see just how important states are, but a curious reader might have noticed a very peculiar thing about the states we've seen so far, that is, they are all frozen in time, unchanging. That is what we're here to rectify today, we're going to push them forwards in time to see not only what they are, but also what they will be.
We will achieve this goal using the

It is recommended to read the paper, as it provides an especially light introduction to the Time evolution operator, but for the stronger of hearts, the
